
Everybody has heard of string theory. Depending on your other interests and prior beliefs, you may either see it a mystical, unattainable orb-like existence atop a fortress, the one true, elegant theory of everything, or a colossal drainage on the worlds’ intellectual resources.
Regardless of the physical ramifications, it is undeniably a mathematically beautiful construction. In this post, I’ll attempt to illustrate, non-technically, some of the aspects and history of string theory. The only thing readers should be aware of prior to embarking on this multi-post adventure is the rough idea of “particles in string theory being vibrations of tiny strings in lots of dimensions”.
The bosonic string
The entrée of string theory is the bosonic theory. This beast operates in 26 dimensions, but does not predict the existence of fermionic particles, at least straightforwardly. In case you need a refresher: fermions are particles with half-integer spin, and constitute matter. For instance, quarks and electrons are both spin $1/2$ particles which associate to build up atoms. The stability of everyday matter is guaranteed by the Pauli exclusion principle for fermions, which as Hawking put it, prevents matter from collapsing to a “soup” of uniform density. Conversely, bosons are particles of integer spin, and mediate forces between the fermions: prime examples include the photon (electromagnetism) and the W boson (mediating the weak force, which among other things is responsible for radioactive decay).
Setting aside the seemingly worrying prospect of a 26-dimensional universe for now, bosonic string theory was nonetheless deemed an unsuitable candidate for developing realistic models of a Theory of Everything due to the absence of fermions. I must confess that this is somewhat anachronistic, with bosonic string theory being developed not out of a desire to unify physics, but rather solve the problem of the then-unexplained strong force in the late 1960s. Now this really is ancient history - the Standard Model as we know it today was hardly complete and new “particles” (which we now know to be certain bound states of quarks) were rearing their heads at particle accelerators every other week. With such an abundance of unexplained experimental data available, it was perhaps the ripest era for theoretical development to follow suit. At the risk of oversimplifying one of the greatest, but now recondite, scientific cold wars, I will plainly state the existence of two major opposing camps: the field theorists and the S-matrix theorists.
While I have a great deal to say about the subject, I will merely say here that the field theorists emerged victorious. Successive triumphs in QCD (quantum chromodynamics, describing gluons) and electroweak theory essentially completed the Standard Model, and their methods persist today. The now-forgotten S-matrix theory (indeed, winners write the history books) should nonetheless be regarded as a pioneer in modern physics. Zooming back onto string theory, the theory’s innovative use of complex angular momenta in Regge trajectories and self-consistent S-matrix “bootstraps” to determine QCD amplitudes eventually, with but a small shift in perspective, culminated in the formation of bosonic string theory.
The theory contains an infinite tower of particles in its spectrum, with ever-increasing masses, each corresponding to a different “vibration” of the fundamental string. Nothing is actually vibrating of course, since in the quantum theory the Fourier modes are promoted to operators which act on a Fock space, but this classical picture is geared for intuition over pedantry.
This tower does not present a problem in itself since, much like the heavy Higgs boson, the heavy particles are surpressed at ordinary energies. What was more worrying was the presence of a particle with negative mass, a tachyon! Unlike the tachyons that pervade science fiction, this particle would not violate causality, but would signal the sickness of the theory in a more subtle way. An important quantum theoretical tool is being able to “approximate” the system as an empty vacuum, and compute corrections from there, order by order. However, the presence of the tachyon is thought to cause the instability of this vacuum, impinging on the consistency of the theory. The effects of the tachyon are actually poorly understood, and may necessitate a more advanced formulation of string theory to “see” the theory from a wider lens. Terrifyingly complicated calculations in the new-fangled “string field theory” lay claim to this.
What can it do?
Nonetheless, this does not present a significant barrier to developing a rich, beautiful theory, stemming from the internal consistencies of the string, and employing an amalgamation of mathematical structures from algebraic geometry, Riemann surfaces and number theory, among others. Perhaps the theory would not be an accurate model of reality, but it could offer tools and hints on how to formulate a theory of everything, once and for all?
It did so in great style. String theory predicted, from first principles, a spin-2 boson called a graviton. This particle would mediate the gravitational force in a quantum theory of gravity, but is currently regarded as hypothetical since it is yet to be observed conclusively. It is actually very simple to write a naïve quantum gravity model analogous to electromagnetism and incorporate it into the Standard Model, but it births untameable divergences in the theory which destroys the predictivity of the model. This is not to say that testable quantum gravity effects cannot be computed - they can be done straightforwardly. But the method to do so, known as effective field theory, necessarily precludes a workable ToE involving gravity: a theory that can operate up to the highest energies, down to the smallest scales.
String theory did this. Consider a closed string, one whose ends are joined up in a loop. Such a string propagating in spacetime traces out a tube-like path. Two such closed strings can fuse together, then split up once more, and this process encodes the interaction between strings. Through the properties of this “worldsheet”, it could be inflated to a sphere with 4 punctures on it - suddenly, the features of graviton scattering could be analysed by looking at this esoteric object! Theorists computed observable effects, and with great joy discovered that all the predicted values were finite. String theory, even in its proto-bosonic form, was a consistent theory of quantum gravity!
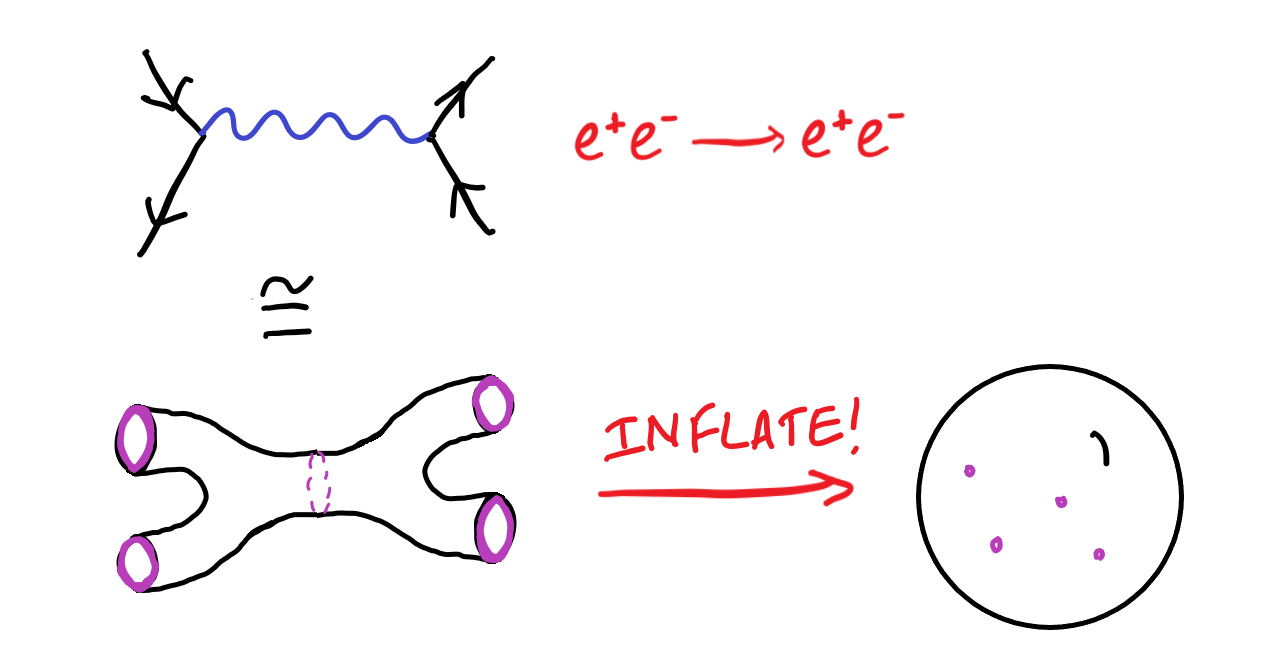
What’s more is that string theory reproduced all existing frameworks: quantum field theory could be recovered by shrinking the length of all the strings to zero, in effect reducing them to ordinary point particles. General relativity emerged in a more intriguing way. The dynamics of the strings meant that a particular quantum field theory lived on the surface of the worldsheet that each string traced out. Moreover, this QFT was special in that the consistency of the string forced it to be scale-invariant (or conformal), so that physics looked the same even if you zoomed in or out. Naïvely it looked like this condition wasn’t satisfied, but this was solved when it was realised that conditions could be imposed on the fields to preserve consistency. These constraints not only implied that the string moved in 26 dimensions, but more miraculously, they reproduced Einstein’s equations of general relativity, complete with smaller stringy corrections! These discoveries reaffirmed the glimmer of hope that string theory, in some incarnation, would solve physics once and for all.
The first critical problem to be solved was introducing fermionic particles into the theory. Beyond some wild speculation that certain chunks of the infinite bosonic spectrum could be melded together to form fermions, it seemed that string theory was dead in the water.
That is, until the discovery of superstrings.