
String Dualities
The five superstring theories that we’ve been constructing are all beautiful, but the fact that there are five of them in the first place is somewhat mysterious. This puzzled string theorists long past the first superstring revolution, but the second superstring revolution brought with it a radical idea - what if all these ostensibly different theories were really related, and so incarnations of a deeper, more fundamental theory?
Let us motivate the nature of these relations with the bosonic string. Recall from last time’s discussion that “string compactification” does not imply topologically manipulating an initial spacetime, but rather positing the exact structure of spacetime right from the get go. Since bosonic string theory operates peacefully in 26 dimensions, choose a spacetime which is a “product manifold” of 24+1D Minkowski space and a 1D circle of some radius $R$. In ordinary terms, the 26th dimension is circular (as a consequence, you can travel in the same direction and come back to your starting point) while the remaining dimensions are flat. Note that despite being circular, this dimension is not necessarily “curled up” in the sense of being comparatively microscopic - this is determined by the radius $R$ which for now remains a free parameter. Now closed strings can wrap around this circular dimension multiple times, akin to a rubber band wrapped around a tube. If a string winds $N$ times around a circle, then clearly it must have a length of at least $2\pi RN$.
The idea of introducing one circular dimension is surprisingly ancient. First proposed by Kaluza in 1921 (general relativity was just beginning to gain traction while the Schrödinger equation had not even been formulated yet!) and refined by Klein, this theory unified gravitation and electromagnetism by hypothesizing a 5D spacetime with the 5th dimension forming a circle. This operated on a purely classical footing, and interestingly, “motion in the fifth dimension” is roughly identified with the charge of the particle. It additionally predicted a dynamical scalar fields, which could serve as a parameter for the expansion of spacetime, or even a coupling between gravity and electromagnetism, depending on the model. This was an early demonstration of how compact dimensions, even at a classical level, can yield exciting new physics.
A main feature of a compact dimension is that momentum along that dimension is quantised: it comes in multiples of $1/R$. This is in contrast to an infinite dimension, where momentum is continuous (this is also clear by taking the $R\to\infty$ limit above - in this limit, a circular dimension unrolls). For the reason, hark back to the quantized momentum levels of a particle in a periodic box - or, if unfamiliar, appeal to the following heuristic description: a particle is described by a wavefunction; with periodic boundary conditions, the particle must form standing waves whose wavelength is a multiple of the box width (other waveforms are suppressed by destructive interference), so wavelength is quantized. But quantum mechanical momentum is inversely proportional to wavelength, so it too is quantized! The $p\propto1/R$ dependence is manifest here - we write that $p=K/R$.
Ordinarily the mass of a particular string state depends on the total number of left-moving excitations and right-moving excitations. However, now that we have a compact dimension, the winding number $N$ and the so-called “Kaluza-Klein excitation number” $K$. The winding number contributes a term $\left(\frac{NR}{\alpha’}\right)^2$ where $\alpha$ is roughly the string tension, while the KK-momentum adds a $\frac KR$ term. Clearly both $N$ and $K$ can be any non-negative integer, depending on the configuration of the string in question.
Here’s the surprising part. What if we had the audacity to switch $N$ and $K$? This would be extremely unexciting were it not for the fact that, upon switching $R$ with $\alpha’/R$ simultaneously, all the formulas remain the same! In other words, compactifying string theory on a circle of radius $R$ yields the same physics as if we were to compactify on a circle of radius $\alpha’/R$. The only difference is that winding numbers and KK momentum number in one theory correspond to KK momentum and winding number in the other - but since both of these could be any non-negative integer anyway, there is no physical difference! Importantly, this $N\Leftrightarrow K, R\Leftrightarrow\alpha’/R$ transform can be equivalently expressed as vertically mirroring the right-moving, but not left-moving, excitations of the string.
Since this forms an equivalence between two rather different looking theories: one string theory (model) whose radius in the 26th dimension is, say, $0.001\text{ m}$, and another whose radius is $1,!000\text{ m}$. This is our first example of a string duality, known as T-duality. This duality will manifest in a deeper form in superstring theory, as we shall see. T-duality also has interesting effects on D-branes, depending on their orientation, but I will not discuss those here.
Let’s start with Type IIA theory. It is more helpful to apply the second incarnation of T-duality: vertically flipping the right-moving modes. Since this is a superstring theory, we only have 10 dimensions to play with, so let’s compactify the 10th dimension on a circle. The right-moving component of the bosonic coordinate is flipped, which also interchanges the winding number and KK-momentum and converts the radius of compactification from $R$ to $\alpha’/R$, as we have seen. As for the partner fermionic coordinate, we would intuitively think that supersymmetry on the worldsheet forces its right-moving part to flip in the same way, and indeed it does. It is important to always keep in mind that applying T-duality never changes the physics, only the mathematical form the theory takes.
But we know that relative signs of fermions play a huge role in distinguishing the two Type II string theories. Indeed, flipping the right-moving sector reverses the chirality of the fermions associated to it. Let’s see what happens to Type IIA string theory as a result. By definition, it has fermions of opposite chiralities amongst its left and right movers. T-duality inverts the compactification radius and flips the chirality of the right-moving fermions, so now we have fermions of the same chirality in both sectors. But this is just the definition of Type IIB string theory! Type IIA compactified on a circle of radius $R$ is the exact same theory as Type IIB compactified on a circle of radius $\alpha’/R$ - they should really be thought of as one unified theory! So unlike in the bosonic case where T-duality related a theory to itself, two different superstring theories are united by this duality.
To relentlessly spring another surprise, it turns out that the two heterotic string theories are also related by T-duality! Here, the analysis is much more difficult and geometric, but it is sound. So another link has been forged, and the castles are no longer isolated.
But there is yet another type of duality. A small motivation (which may not actually be very enlightening, but is a fun morsel nonetheless) can be seen if we beam ourselves down to ordinary electromagnetism. In its classical, non-covariant formalism, there are two fields - the electric and the magnetic - permeating throughout space, interacting with charged particles. The evolution of such fields with time is determined by Maxwell’s equations - for instance, the evolution of the electric field is determined by the charge distribution and the rate of change of the magnetic field. If we take the simple cases where no charges or currents exist (the theory may seem trivial, but it still allows for the propagation of electromagnetic waves), then Maxwell’s equations show a surprising symmetry of sorts: if you interchange (roughly) the electric field with the magnetic field, the equations remain the same. As it turns out, an analogue of this relation carries forth to supersymmetric gauge theories and string theory, where it is christened S-duality.
The main way to practically compute quantities in string theory is to “expand the theory in $\alpha’$”. What this means is that we recognise that the string is an extended (not point) object, and this presents computational difficulties, so we initially pretend it is a perfect point particle and layer on stringy corrections on top of this. It is akin to approximating a function by a Taylor expansion in ordinary calculus.
However, there is also another type of expansion that we must factor in: that of string interactions. The strength of interactions is described by the value $g_s$, the string coupling constant. Roughly, a small value of $g_s$ describes a system in which strings interact weakly, and so we can Taylor expand from the free, non-interacting theory as a base point, which itself serves as a good approximattion. However, at high $g_s$, the strings are strongly coupled, and the analysis becomes very complicated since strings are continuously interacting, and it becomes difficult to entangle them, so to speak. Coupling constants are of course ubiquitous in quantum field theory as well. In quantum electrodynamics, the coupling constant is proportional to the square of the electron’s charge, with some more fundamental constants added in too. This coupling constant is weak, at around $1/137$ (dimensionless), which means that approximating the theory as non-interacting, then adding corrections for the interactions weighted by powers of the coupling constant is valid, and indeed this is how computations are performed. However, quantum chromodynamics has a coupling constant which is around $1$, and so this series method breaks down as the additional terms in the series all have the same size, so we won’t ever be able to get a good approximation by truncating this sum at some point. Consequently, non-perturbative methods which do not rely on performing this sum are utilised, such as lattice QCD, in which spacetime is discretised and the lattice spacing is then taken to zero in order to recover continuous spacetime (this is a huge subfield of its own). String theory differs from the above in that the value of this coupling constant is determined dynamically by the value of a particular scalar field known as the dilaton: $g_s =\exp\langle\Phi\rangle$, or in words, the strength of the string interaction is determined by the average value of the dilaton field in a vacuum. Like all quantum fields, the dilaton is subject to quantum fluctuations, but in this definition we average over all such fluctuations.
Returning to string theoretic apprxomations, we may additionally opt to neglect string states with high mass, as they are very difficult to produce and so do not contribute substantially to observable quantities, at least at low energies below their production level. In the extreme limit, we can disregard all states with mass and simply consider the massless fields, while taking $\alpha’\to 0$. This creates the low-energy effective action of string theory, which is seen to be supergravity (SUGRA) in 10D, as I have mentioned before. However, the validity of SUGRA only extends as far as low to intermediate energies - it is seen to break down at high energies, which signals that there must be a more complete thoery which subsumes it. Indeed, the various string theories form these UV-completions of the different supergravities.
SUGRA tends to be easier to manipulate, and we can identify tools and hints of physics that goes on in string theory, even if we cannot directly extrapolate results. In particular, consider the low-energy effective actions of type I and $\mathrm{SO}(32)$ heterotic theory. Their mathematical forms are extremely similar, as they are related via negating the dilaton field ($\Phi\Leftrightarrow-\Phi$) and conformally scaling the metric (the metric is the field which determines the spacetime geometry, including distances, angles and of course gravitational effects). This conformal scaling preserves the angles of the spacetime geometry but alters distances non-uniformly - this merely suggests that the two different spacetimes are mapped to each other. Once again, since string theory allows any spacetime to serve as a background (provided of course that they are consistent with Einstein’s equations of general relativity, which the conformal rescaling preserves), this is a perfect symmetry of the two theories.
The negation of the dilaton is extremely important. If we pretend that this relation holds not only for supergravity, but also for the entire string theory, then since the string coupling constant is determined by $\exp\langle\Phi\rangle$, we see that a coupling of $g_s$ in type I would correspond to a coupling of $1/g_s$ in $\mathrm{SO}(32)$ heterotic. In other words, S-duality is suggesting that strongly coupled interactions in one theory can be described by weakly coupled interactions in the other theory. As a result, they should once again be regarded as two facets of the same underlying theory.
From this we can conclude with certainty that type I string theory and $\mathrm{SO}(32)$ heterotic theory are equivalent when probed at low energies. But does this duality extend to the full string theory at all energies? This is diffcult to check directly, since by definition probing the effects of strongly coupled string interactions (to verify the duality) is intractable. However, there are certain tests that rely on non-perturbative effects, for example, matching the tension of D-branes on either side of the duality. So far, S-duality has passed all tightly-constraining theoretical checks, and is regarded as an exact duality. However, we do not have a 100% rigorous proof for this, unlike T-duality which is very easy to verify. This method of conducting theoretical consistency checks to verify S-duality is a general feature of such dualities in supersymmetric gauge theories.
The final manifestation of duality in string theory is once again an S-duality, but this time it concerns type IIB string theory. The spectrum of this theory includes within it a massless dilaton $\phi$ (every string theory does, in the bosonic sector) but also a massless scalar field $C_0$ from the fermionic sector, known as an RR zero-form gauge field. This feature is unique to type IIB, and means that it has a symmetry that mixes the two fields into each other. Interestingly, due to stringy effects, the symmetry is not continuous (like a rotation), but rather discrete (like translation along a lattice). One such discrete symmetry transformation, when evaluated at vanishing $C_0$, once again flips the sign of the dilaton, which as we have seen corresponds to sending the coupling constant $g_s$ to $1/g_s$. So S-duality implies that Type IIB string theory is self-dual, and strongly coupled effects can be described by effects at weak interactions, and vice versa.
This concludes the beautiful web of dualities that connect and unify all the superstring theories. They are mathematically breathtaking, and will be studied for years to come.
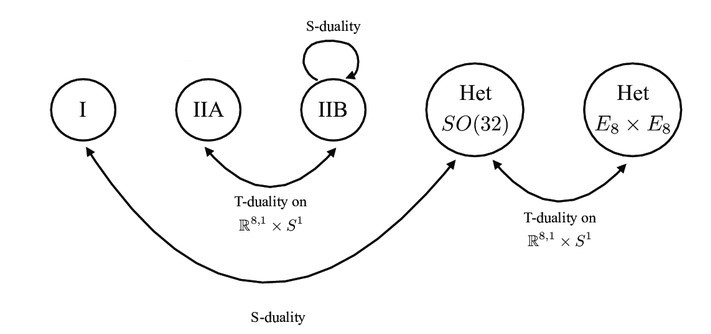
But I leave you on one note. All 5 string theories are now connected. Can we build one single fundamental, underlying description of all of them together? Would such a theory be consistent? What would it look like? How would it reduce to the existing string theories? Tell us more!
Edward Witten in 1995 told us the answer. The fundamental theory, uniting all of string theory together, operates in 11 dimensions. They call this beast M-theory.
But it is not a theory of strings…