Definitions and History
Let’s talk about electrons. Classically, you can model them as a ball of charge whose radius is determined by equating the electrostatic potential energy that it generates with its rest mass energy. Now interestingly we find that an electron interacts with a magnetic field - something that we would expect from a rotating charged body. But the magnitude of angular momentum that is consistent with experimental observations of the electrons in magnetic fields would imply that either the charge or the mass of the electron is rotating faster than the speed of light - a clear violation of special relativity.
Later quantum mechanics emerged as a more accurate paradigm, and preliminary results could provide a partial resolution of these problems. In quantum mechanics, the electron is diffused as a probability cloud and has an intrinsic angular momentum known as spin, even though it’s not physically spinning! This spin also coupled to the magnetic field, and could provide an explanation for the observed deviation of an electron in Penning traps. If you would like to learn more, the Stern-Gerlach experiment was one of the landmark experiments in adopting the idea of spin.
The magnitude of interaction of an electrically charged fundamental particle with an external magnetic field is characterised by its magnetic moment - and this value depends on the mass, charge and other fundamental properties of the given particle. In particular, the magnetic moment of spin-1/2 particles (like the electron) can be characterised by a single number knbown as the g-factor. Classical theory predicts a magnetic moment of g-factor for the electron, but this is off by a factor of about 2. Quantum considerations involving the Dirac equation (a relativistic extension of the ubiquitous Schrödinger equation) yield a magnetic moment of 2, and this prediction was a huge success for the early architects of quantum mechanics, although it was still off by about 0.1% from its measured value of 2.002319304… - and this was puzzling for quite a while.
Quantum field theory?!
The ultimate answer came from quantum field theory - specifically, quantum electrodynamics, as developed simultaneously by Schwinger, Tomonaga, and of course Feynman. In essence, all fundamental particles are excitations of the underlying fundamental field permeating through spacetime (so for instance an electron is a “ripple” in the electron field). The reason for the deviation of the QFT magnetic moment from the previous results is quite technical, so rather than providing a misleading explanation using “a seething pot of virtual particles” (::shudders::), I will explain it like this: imagine two theories: one in which no particles interact (photons just propagate as waves, electrons are uncharged), and one in which interactions are turned on (now electrons can attract each other and emit photons when they decelerate!). Intuitively (or maybe not), the vacua of these two theories look wildly different to each other, since the coupling of the fields to each other differs, with the vacuum of the free theory (the “free vacuum”) being a lot simpler.
Even though photons and electrons interact in, well, the interacting theory, the Dirac equation analysed their contribution to the g-factor by pretending they lived in the free vacuum, which makes calculations relatively simple. Of course, the correct g-factor value can only be obtained if we look at electron-photon interaction in the true, interacting value - but with all of its non-linearities, this is easier said than done. Thankfully, the interaction strength of the electromagnetic force is quite small (it is $\alpha=\frac{1}{137}$, whereas the strength of the strong nuclear force mediated by the gluon is $\sim 1$), and this makes it amenable to a power series solution in $\alpha$. You may have seen something similar while solving differential equations using Taylor series - but if not, you can think of it as dividing the answer into pieces that get progressively smaller but progressively harder to calculate. In this context, we have the heuristic equation
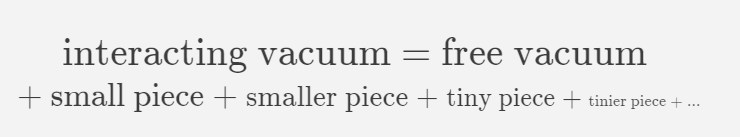
Each of the smaller pieces can be computed through calculating certain scattering processes of the electrons and photons in the free vacuum, and is proportional to increasing powers of $\alpha$. (In reality the series is a bit more complicated: if you would like a technical account on how it works in the context of the g-factor, then see my Physics.SE answer here).
The process of actually calculating these small pieces relies on the techniques of quantum field theory, and is ostensibly a bunch of extremely complicated and often divergent integrals that one has to make sense of. Feynman found a way to illustrate these integrals in a simple manner, through his diagrams (though they’re still very difficult to understand and compute!).
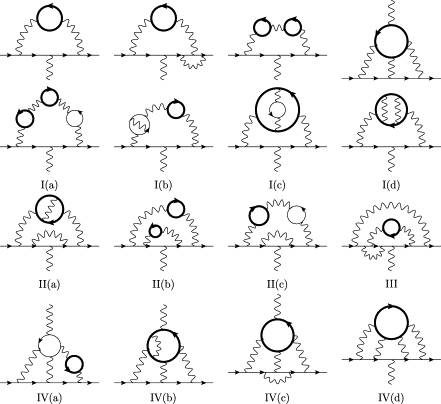
If you look at the previous diagram, you’ll notice that the only lines are an arrow going in, an arrow going out, and a squiggly line. The former two represent the electron, and the last is a photon. This represents the intuitive notion that the magnetic moment can be calculated by looking at what happens to an electron in an external electromagnetic field (specifically, the magnetic part).
The diagram series
These Feynman diagrams can be grouped according to the number of vertices that they have - and the sum of all the diagrams in one group is, roughly, a function of $\left(\frac\alpha\pi\right)^{v-1}$ where $v$ is the number of vertices. So with increasing vertices, the diagrams contribute a smaller amount, and adding up all of these gives us the precise value. Unfortunately, even at 5 vertices there are some 10,000 different diagrams, but computers have managed to do this explicitly.
Schwinger, Feynman and Tomonaga all discovered the first order result independently, and presented their findings at the APS meeting in January 1948:
This was an improvement over Dirac’s result of $g=2$ by 3 significant figures, and a triumphant confirmation of the success of QFT. Indeed, the value $\frac{\alpha}{2\pi}$ is engraved on Schwinger’s gravestone.
One quibble: naturally, one would imagine that the other fundamental fields in the Standard Model (say, the gluon field) might also modify the electon g-factor. As it turns out, these contributions are negligible due to the small electron mass - but the mystical muon provides an avenue to incorporate these corrections, and brings with it the alluring possibility of discovering new physics. Stay tuned for more.