
In the last post, I described bosonic string theory and its limitations. A natural method to augment the theory is to introduce supersymmetry, an established idea from quantum mechanics.
A Foray into Supersymmetry
It is imperative to take a momentary step back and describe supersymmetry in general, unrestricted to the confines of stringy physics. The premise is straightforward: supersymmetry posits the existence of one (or more!) particles corresponding to each existing particle in the model. The kicker is that this partner has the opposite “statistics”, meaning that a boson will be paired with a fermionic superpartner and vice versa. For such a radical proposal, it is somewhat puzzling that physicists place a great deal of faith in its existence!
Here’s why - supersymmetry automatically solves many pressing unresolved problems lurking in the Standard Model, including the small value of the Higgs boson relative to its theoretically expected value (it weighs in at a hefty 125 GeV, nonetheless). Furthermore, it modifies the behaviour of the fundamental forces (electromagnetic, weak and strong), causing them “align” at high energies and thus setting the stage for a grand unification, wherein all the forces are seen to be aspects of a single, unified, fundamental force, and their diverging characters emerge at low energies due to another Higgs mechanism. Now without supersymmetric corrections, the “couplings” of these forces come tantalisingly close, provoking mystery at this unnaturally small offset. This is probably the paramount empirical support of supersymmetry, the other compelling feature propelling it beyond its adversaries being that it makes no changes to ordinary energy physics, and so is immediately compatible with the Standard Model and the substantial experimental checks it has been subjected to. Among other things, this unification predicts that the proton is unstable, and can decay to two lighter particles: an antielectron and a pion. Finally, certain attractive supersymmetric models provide clear-cut candidates for dark matter - the lightest supersymmetric partners of neutrinos.
Experimental observations have not treated this conjectured symmetry lightly. While the LHC could validate the existence of the Higgs boson, it could not find a trace of superparticles, to much disbelief. Proton decay experiments have been conducted for years with tonnes of heavy water in salt mines, but have yielded negative results. Lest one cast premature aspersions on the theory, let me quickly add that these results present no significant blow to supersymmetry - the supersymmetric scale could simply be higher than the energies probed by the LHC.
Least troubled by the news were the mathematically-inclined theoreticians - SUSY is a prized member of many a toolkit. With seemingly more chaos with the introduction of more particles, it may be surprising that supersymmetric theories are often simpler than the base model! This is because SUSY constrains the theory, placing restrictions on its freedom to foster complexity. Take quantum chromodynamics, a consumer of millions of supercomputer hours a year. Rigorous, mathematically sound descriptions of the mass gap, confinement, and strongly coupled behaviour at low energy are thorns in the otherwise beautiful, “non-abelian gauge” theory. If anyone proclaims otherwise, they are kindly advised to claim their $1 million from the Clay Mathematics Institute. But when supersymmetrised, the resulting SQCD suddenly becomes amenable to mathematical torture and inspection, and what’s more, we can probe the strong coupling effects exactly! As a crazier example, consider “$\mathcal N=4$ Super Yang Mills” theory - this is the most symmetric theory without gravity in 4 dimensions, with each particle having four superpartners. The Lagrangian is as cool as the name:
$$
L = \operatorname{tr} \left\{-\frac{1}{2g^2}F_{\mu\nu}F^{\mu\nu}+\frac{\theta_I}{8\pi^2}F_{\mu\nu}\bar{F}^{\mu\nu}- i \overline{\lambda}^a\overline{\sigma}^\mu D_\mu \lambda_a -D_\mu X^i D^\mu X^i
+g C^{ab}_i \lambda_a[X^i,\lambda_b] + g \overline{C}_{iab}\overline{\lambda}^a[X^i,\overline{\lambda}^b]+\frac{g^2}{2}[X^i,X^j]^2 \right\}
$$
Incredible though it may seem, this theory is completely conformal, or scale-invariant, meaning that it looks the same zoomed in or out (were you paying attention in the previous blog post?) and as such, it is often used a toy model, especially in higher-dimensional physics.
The Superstring
Speaking of higher dimensional physics, this detour has lit the path for resolving the fermion problem in string theory: we ought to pepper in supersymmetry to get a consistent, all-encompassing, finite, quantum-gravitational theory. Since this is easier said than done, revisiting our dear friend the bosonic string offers us a moment of solace. Though I did not mention this very explicitly in the previous post, there are two clearly different types of strings: open strings, with free ends, and closed strings, whose ends are joined to form a loop. Now a theory with open strings is necessarily a theory with closed strings, because an open string can move in a circle to trace out a cylinder. But this is just the worldsheet for a closed string propagating! Bear in mind that the converse does not hold: there is no mechanism for a closed string to snap into an open one, and so there can exist theories of only closed strings.
The analysis of the closed string spectrum is roughly equivalent to analysing two copies of the open string, combined together. This can be thought of as vibrations on a looped string being a combination of left-moving waves and right-moving waves, at least classically. The coordinate on the string is naturally intepreted as a bosonic field and the usual quantization procedure (using the dictionary from ordinary quantum mechanics to translate a classical theory into its quantum counterpart) yields bosonic string theory, described in the previous post.
However we return to the battle, war-hardened and bruised with fermionic deficiency, this time brandishing supersymmetry (perhaps a little too fiercely, could you tone it down a notch?). And this dictates that we add a fermionic coordinate as a superpartner to the bosonic coordinate, for both the left-moving and right-moving modes. We simply analyse each set of modes separately, eventually combine them together and several pages of mathematical toil later, we’ve done it. We’ve constructed superstring theory (or rather, Green and Schwarz did, 30 years ago).
Or have we? There are really two pictures associated to string theory, one of string floating around, interacting in a high-dimensional spacetime, and one defined by two-dimensional interacting quantum field theories on donut-like surfaces forming the string worldsheet. Ontologically, string theory does not make a distinction between the two. But the supersymmetric supplement that we added above is only for the worldsheet theory. The string spectrum is not supersymmetric in spacetime. But if we want string theory to be an accurate description of reality, it should have spacetime supersymmetry to reduce to the field-theoretic picture described previously! A deeper analysis suggests more gripping problems: there is still a tachyon in the theory, and the presence of a massless gravitino in the theory (the superpartner of the graviton) leads to a breakdown of causality and some sacred mathematical tenets of the theory if spacetime supersymmetry is not present.
At this stage it seems string theory is well and truly done for. But the emotional rollercoaster continues. Gliozzi, Scherk and Olive discovered that in order to upgrade this currently non-physical theory to a consistent one, one must truncate the space of states by enacting the GSO projection. Amazingly, this solves every single one of the problems presented thus far. The tachyon does not survive the projection; it is removed from the theory. The number of degrees of freedom at each mass level match between the bosonic and fermionic sector, the coveted spacetime supersymmetry has been obtained, and causality and “gauge invariance” are restored. Superstring theory has finally come to life.
But wait (oh no…). Recall how the closed string is composed of left-moving and right-moving parts? Well, I conveniently forgot to mention that there are two inequivalent choices of GSO projection, and we are free to choose either the same or different ones for each direction. This means we have constructed not one, but two superstring theories!
But why? What’s the difference? Well that’s a story for another blog post.

Everybody has heard of string theory. Depending on your other interests and prior beliefs, you may either see it a mystical, unattainable orb-like existence atop a fortress, the one true, elegant theory of everything, or a colossal drainage on the worlds’ intellectual resources.
Regardless of the physical ramifications, it is undeniably a mathematically beautiful construction. In this post, I’ll attempt to illustrate, non-technically, some of the aspects and history of string theory. The only thing readers should be aware of prior to embarking on this multi-post adventure is the rough idea of “particles in string theory being vibrations of tiny strings in lots of dimensions”.
The bosonic string
The entrée of string theory is the bosonic theory. This beast operates in 26 dimensions, but does not predict the existence of fermionic particles, at least straightforwardly. In case you need a refresher: fermions are particles with half-integer spin, and constitute matter. For instance, quarks and electrons are both spin $1/2$ particles which associate to build up atoms. The stability of everyday matter is guaranteed by the Pauli exclusion principle for fermions, which as Hawking put it, prevents matter from collapsing to a “soup” of uniform density. Conversely, bosons are particles of integer spin, and mediate forces between the fermions: prime examples include the photon (electromagnetism) and the W boson (mediating the weak force, which among other things is responsible for radioactive decay).
Setting aside the seemingly worrying prospect of a 26-dimensional universe for now, bosonic string theory was nonetheless deemed an unsuitable candidate for developing realistic models of a Theory of Everything due to the absence of fermions. I must confess that this is somewhat anachronistic, with bosonic string theory being developed not out of a desire to unify physics, but rather solve the problem of the then-unexplained strong force in the late 1960s. Now this really is ancient history - the Standard Model as we know it today was hardly complete and new “particles” (which we now know to be certain bound states of quarks) were rearing their heads at particle accelerators every other week. With such an abundance of unexplained experimental data available, it was perhaps the ripest era for theoretical development to follow suit. At the risk of oversimplifying one of the greatest, but now recondite, scientific cold wars, I will plainly state the existence of two major opposing camps: the field theorists and the S-matrix theorists.
While I have a great deal to say about the subject, I will merely say here that the field theorists emerged victorious. Successive triumphs in QCD (quantum chromodynamics, describing gluons) and electroweak theory essentially completed the Standard Model, and their methods persist today. The now-forgotten S-matrix theory (indeed, winners write the history books) should nonetheless be regarded as a pioneer in modern physics. Zooming back onto string theory, the theory’s innovative use of complex angular momenta in Regge trajectories and self-consistent S-matrix “bootstraps” to determine QCD amplitudes eventually, with but a small shift in perspective, culminated in the formation of bosonic string theory.
The theory contains an infinite tower of particles in its spectrum, with ever-increasing masses, each corresponding to a different “vibration” of the fundamental string. Nothing is actually vibrating of course, since in the quantum theory the Fourier modes are promoted to operators which act on a Fock space, but this classical picture is geared for intuition over pedantry.
This tower does not present a problem in itself since, much like the heavy Higgs boson, the heavy particles are surpressed at ordinary energies. What was more worrying was the presence of a particle with negative mass, a tachyon! Unlike the tachyons that pervade science fiction, this particle would not violate causality, but would signal the sickness of the theory in a more subtle way. An important quantum theoretical tool is being able to “approximate” the system as an empty vacuum, and compute corrections from there, order by order. However, the presence of the tachyon is thought to cause the instability of this vacuum, impinging on the consistency of the theory. The effects of the tachyon are actually poorly understood, and may necessitate a more advanced formulation of string theory to “see” the theory from a wider lens. Terrifyingly complicated calculations in the new-fangled “string field theory” lay claim to this.
What can it do?
Nonetheless, this does not present a significant barrier to developing a rich, beautiful theory, stemming from the internal consistencies of the string, and employing an amalgamation of mathematical structures from algebraic geometry, Riemann surfaces and number theory, among others. Perhaps the theory would not be an accurate model of reality, but it could offer tools and hints on how to formulate a theory of everything, once and for all?
It did so in great style. String theory predicted, from first principles, a spin-2 boson called a graviton. This particle would mediate the gravitational force in a quantum theory of gravity, but is currently regarded as hypothetical since it is yet to be observed conclusively. It is actually very simple to write a naïve quantum gravity model analogous to electromagnetism and incorporate it into the Standard Model, but it births untameable divergences in the theory which destroys the predictivity of the model. This is not to say that testable quantum gravity effects cannot be computed - they can be done straightforwardly. But the method to do so, known as effective field theory, necessarily precludes a workable ToE involving gravity: a theory that can operate up to the highest energies, down to the smallest scales.
String theory did this. Consider a closed string, one whose ends are joined up in a loop. Such a string propagating in spacetime traces out a tube-like path. Two such closed strings can fuse together, then split up once more, and this process encodes the interaction between strings. Through the properties of this “worldsheet”, it could be inflated to a sphere with 4 punctures on it - suddenly, the features of graviton scattering could be analysed by looking at this esoteric object! Theorists computed observable effects, and with great joy discovered that all the predicted values were finite. String theory, even in its proto-bosonic form, was a consistent theory of quantum gravity!
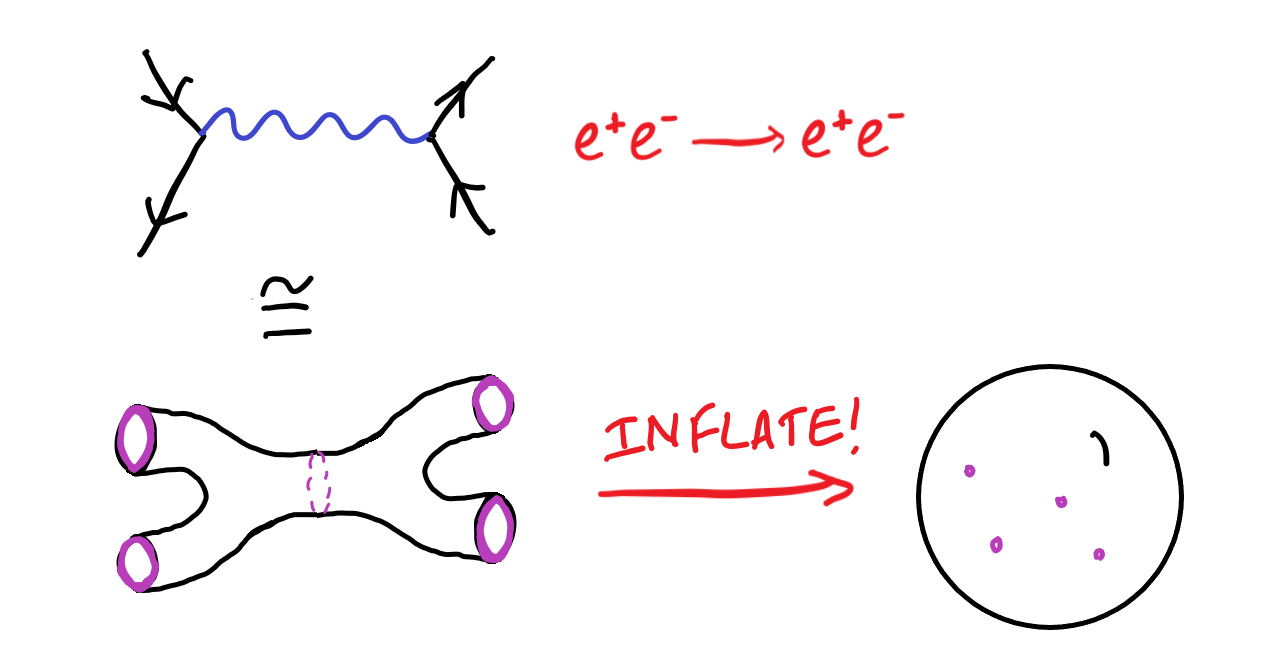
What’s more is that string theory reproduced all existing frameworks: quantum field theory could be recovered by shrinking the length of all the strings to zero, in effect reducing them to ordinary point particles. General relativity emerged in a more intriguing way. The dynamics of the strings meant that a particular quantum field theory lived on the surface of the worldsheet that each string traced out. Moreover, this QFT was special in that the consistency of the string forced it to be scale-invariant (or conformal), so that physics looked the same even if you zoomed in or out. Naïvely it looked like this condition wasn’t satisfied, but this was solved when it was realised that conditions could be imposed on the fields to preserve consistency. These constraints not only implied that the string moved in 26 dimensions, but more miraculously, they reproduced Einstein’s equations of general relativity, complete with smaller stringy corrections! These discoveries reaffirmed the glimmer of hope that string theory, in some incarnation, would solve physics once and for all.
The first critical problem to be solved was introducing fermionic particles into the theory. Beyond some wild speculation that certain chunks of the infinite bosonic spectrum could be melded together to form fermions, it seemed that string theory was dead in the water.
That is, until the discovery of superstrings.
Roadmap for General Relativity
The best thing about general relativity is that it can be learned concurrently to the standard quantum route (quantum mechanics, statistical mechanics, quantum field theory, supersymmetry). I personally found general relativity to be easier to learn than quantum field theory, at least at a ~4th year undergraduate level. This was probably due to my prior interest in mathematics: general relativity requires a much, much broader maths background than QM, but once you acquire an intuitive visualisation of differential geometry concepts, it aids the learning process significantly.
Definite prerequisites
-
Special relativity: Unlike for QFT, here you have to know special relativity in and out, 100%. SR is a very problem-solvey kind of subject, so it helps to do all the practice you can get. I also recommend reading a bit about the ontological differences between SR and GR prior to diving in head first - I paired this with a historical account of Einstein’s development of GR (modern sources present it in a much cleaner way mathematically, but this slightly conceals what Einstein’s motivations and thought process were)
-
Newtonian Gravity: Goes without saying. Make sure to have worked with the potential formalism, and find out some of its conflicts with general relativity right away.
-
Multivariable calculus: When a theory operates in 4 dimensions, you know you’re gonna need at least multivariable calculus. In addition, you need to be solid with differential equations and basic PDE (that’s quite literally what the Einstein field equations are)
-
Tensor calculus: Constructing and analysing Lorentz covariant objects is critical, as is seeing how quantities change after coordinate transformations. This does require a background in abstract (multi) linear algebra, particularly vector spaces, their duals, changing basis, multilinear maps, tensor products, etc. Tensor manipulations in GR are actually simple to do in practice (once you get the hang of the notation) but they encode quite a bit of information, so it is important to know what you’re doing. I recommend you master this before even opening a GR textbook.
-
Real Analysis: The quintessential tedious but necessary precursor to “actual maths”. Actually thinking about spacetime topology is something you won’t have to do right from the beginning, but of course metric spaces, differentiable maps, etc. are the basis for introducing differential geometry. My advice? Don’t sweat it, a basic understanding is all that’s required, you certainly don’t need to have solved every problem in Munkres.
-
Differential Geometry: My recommendation will stray from the conventional wisdom. I recommend that if you have even a remote mathematical inclination, you become proficient in basic differential geometry before commencing with any serious GR. I usually recommend people learn mathematics in the context of physics if they can, since that physical context provides intuition, but I don’t think the tenets of GR have any significant insight to provide in this case. By “basic”, I mean manifolds, frames, parallel transport, covariant derivatives, curvature. A lot of this has quite a bit of overlap with what others call “tensor calculus”.
-
Electrodynamics Theory: Maxwell’s equations in Lorentz-covariant form, stress-energy tensor, EM Lagrangian. These are useful for illustrating analogous constructions in GR. Note that I’ve qualified this with the word “theory” to emphasise that “only” a mathematical background in E&M (as opposed to augmented with physics-style tricks and techniques) is sufficient.
Learn it along the way (or before, for a better understanding):
-
Electromagnetic waves: The clear-cut cousin of gravitational waves, clearly not a prerequisite but it is useful to know about vectorial polarisation before upgrading to tensorial gravitational polarisation.
-
Classical field theory: Action principles, symmetries, conservation laws - all very helpful in understanding GR as a field theory. Formulating GR as a gauge theory is a very nice rabbit hole to pursue, and tools like the Hilbert action and Palatini formalism are powerful to have your disposal. You will need predominantly Lagrangian mechanics here (the features of a diffeomorphism-invariant theory are really intriguing on this front), but experts in the Hamiltonian formalism can take a look at the ADM formalism, which feeds right into canonical quantum gravity.
-
Gauge theory: For those people who heard “covariant derivative” and immediately assumed GR was a Yang-Mills theory. There are lots of nice analogies, and many key differences between the two. Principal and vector bundles find great use in this regard.
-
Basic cosmology: Why not? Even if you’re a diehard spacetime structure theorist and hate our actual universe, cosmology ties together E&M, quantum mechanics and gravity in a wonderfully tangible, physics-y manner.
-
Anything on the quantum track - there is zero interplay between curved spacetime and quantum effects for a long, long part of the learning curve, so you can dip your toes in both simultaneously guilt-free.
Roadmap for Quantum Mechanics
In the context of beginners’ pedagogy, the venerable quantum mechanics gets a bad rap because of the abundance of pop-sci articles ranging between misleading to downright incorrect. Luckily the existence of Griffiths’ introductory quantum mechanics textbook means that you can learn practical, fundamental quantum mechanics without picking up misinformation. Once you’ve pinned down the basics (say, until time-dependent perturbation theory), I suggest immediately moving to Sakurai’s textbook or Littlejohn’s notes for 221AB, and learning everything again. I’m serious - it’s essential to redo it rigorously, but the introductory content from Griffiths’ will allow you to rapidly grasp the material in a more advanced textbook.
Definite Prerequisites:
-
Multivariable calculus: You need to be pretty comfortable with differentiating and integrating functions of multiple variables, since that’s what wavefunctions are. It goes without saying that prior to this you should be fluid with Calc I and Calc II. Periodic functions and Fourier transforms also play a crucial role in quantum mechanics - you should be able to visualise all of these notions very well, the intuition will take you far. Also it leads up to:
-
Differential equations: Separation of variables, First-order, Second-order homogenous linear ODEs, and some basic understanding of PDEs. Why? Because the Schrödinger equation, a cornerstone of QM, is literally a linear PDE. You’ll get to learn cool analytical techniques to solve a variety of systems along the way.
-
Matrices and vectors: You should know how to multiply matrices, diagonalise them, all that jazz. A lot of the time, quantum mechanics actually operates in infinite-dimensional Hilbert spaces, and operators essentially turn into “infinite-dimensional matrices”. Luckily, many (but not all!) notions from finite-dimensional linear algebra carry over fairly smoothly, so you need not have learnt anything about these mysterious creatures while jumping in.
-
Classical mechanics: Can’t “go quantum” before you have a handle on the physics of ordinary objects! I’m not saying you need to be intimately familiar with infinite pulley diagrams; more important is a brief background in the Hamiltonian formalism of classical mechanics. It’s best to go through this a few times, so that even if all you remember is “Hamiltonian = time translations” while coming into QM, revisiting those notions in a different light should concretise your understanding.
Learn it along the way (or before, for a better understanding):
-
Functional analysis: The big brother of linear algebra. Operator theory, Hilbert spaces, C* algebras, spectral theory, distributions, von Neumann. Forbiddingly dry if presented wrong, but illuminating and powerful when done right. Best served with a smattering of quantum mechanical “paradoxes” arising from trying hopelessly to abstract the properties of finite-dimensional matrices to continuous spaces.
-
Electrodynamics: Probably not the most crucial one here, to be honest. Knowledge of Maxwell’s equations and interactions of electric and magnetic fields with matter is just about it: a lot of electrodynamics consists of tools for problem solving, and gaining a qualitative understanding takes a lot less effort than poring through Jackson.
-
Path integrals: essentially a (rather large) offshoot of Green’s functions. Some basic measure theory can’t go amiss here, and it is very helpful for quantum field theory later on.
-
Lie groups/algebras and representation theory: This is a deep, beautiful subject, and one of my favourite areas in mathematics. It illuminates the otherwise impenetrable concept of spin; ladder operators, particle classicification, angular momentum, simplifying systems using symmetry, multiparticle systems, “generators” of symmetries, Clifford algebras - the list goes on and on.
-
Classical symplectic geometry: It’s always fun to see the correspondence between ordinary Poisson brackets and commutators. More seriously, ideas like Hamiltonian vector fields, moment maps and the symplectic form play a key role in demystifying quantum mechanics. A lot of enthusiasts also go the other way, first learning quantum mechanics and then the Hamiltonian formulation. But if you can delay this gratification, then I definitely suggest doing the converse. Also see: Dirac’s quantization of gauge systems (if you learn from Dirac’s textbook, this is the foundation stone anyway)
-
NumPy, MATLAB or Mathematica! Very few people are capable of whipping up illuminating visualisations of complex (heh) quantum phenomena. Even creating a animation of tunneling through a barrier and the Fourier transform of the wavefunction is fantastic fun, and it’ll be very powerful to have these tools at your disposal for clarity and visual understanding

